BYU logo Computer Science
CS 465 Introduction to Security and Privacy

Password authentication

Ungraded Quiz

  • Why should websites always hash the passwords they store?
  • What role does the salt play when hashing passwords?
  • Why should a password hashing algorithm be relatively slow?
  • Why can the concept of entropy lead to misleading conclusions about password security?

Key concepts

Password authentication

  • never store passwords as cleartext — if your password database is stolen, the attacker now knows all passwords and can try them on other sites

  • instead store hash of the password, using a cryptographic hash function

  • dictionary attack

  • offline vs online attacks

  • password capture — shoulder-surfing, keyloggers, malware, phishing, social engineering

  • password interface bypass

  • defeating recovery mechanisms

  • password composition policies are designed to help users pick passwords that are “stronger” by requiring minimum lengths and different types of characters (uppercase, lowercase, digits, special characters)

  • see advantages and disadvantages of passwords

Not only does no known scheme come close to providing all desired benefits: none even retains the full set of benefits that legacy passwords already provide. In particular, there is a wide range from schemes offering minor security benefits beyond legacy passwords, to those offering significant security benefits in return for being more costly to deploy or more difficult to use. We conclude that many academic proposals have failed to gain traction because researchers rarely consider a sufficiently wide range of real-world constraints.

Password-guessing strategies and defenses

  • system administrators should use rate-limiting to throttle online guessing attacks

  • system administrators should use salting and hashing to slow down offline guessing attacks

    • hashing should be iterated, meaning using multiple rounds, e.g. 1000 rounds of hashing — longer hashing times make it harder for the attacker to brute force guess passwords from a database breach
    • hashing should use a salt to combat dictionary attacks
    • hashing should use a specialized password-hashing function, e.g. Argon2

  • system administrators may use a pepper — like a salt, but stored separately, e.g. in an HSM (hardware security module)

  • system administrators should check user passwords against breach databases to limit daamage from online and offline guessing attacks

See OWASP Password Storage Cheat Sheet

  • user chosen passwords are not random

Entropy

  • information-theoretic entropy (Shannon’s entropy) conveys how much information is revealed by an event
  • takes into account all possible events and their probability
  • often misused for passwords, leading to poor conclusions about password security

Example (from textbook)

Let X be a random variable taking values from rolling a fair eight-sided die. Outcomes X = 8 all have qi = 18

  • H(X) = lg(8) = 3 bits.

For a fair six-sided die, qi = 16

  • H(X) = lg(6) = 2.58 bits.

If the six-sided die instead has outcomes X = {1,2,3,4,5,6} with resp. probabilities 1/2, 1/4, 1/8, 1/16, 1/32, 1/32,then H{1/2,1/4,1/8,1/16,1/32,1/32}=1/2·1 + 1/4·2 + 1/8·3 + 1/16·4 + 2(1/32·5)= 1.9375 bits, which, as expected, is less than for the fair die with equiprobable outcomes.

Example (taken from an unnamed website)

E = L×log2(R)

  • E is your password entropy
  • R is the possible range of character types in your password
  • L is the number of characters in your password (its length)
ExampleCharacter RangePassword LengthCalculationBits of Entropy
Bankruptcies5212 chars.E = 12 x 5.768.4
1Bankruptcies26214 chars.E = 14 x 5.9583.3
1Bankruptcies2&%9416 chars.E = 16 x 6.55104.8
  • Generally, a strong or high-entropy password scores at least 75 bits. Anything measuring fewer than 72 bits is reasonably easy for a machine to crack.

Why this approach is misleading

  • assumes attacker goes through every possible password, methodically
    • in reality, attackers try high probability passwords first
  • assumes we know the probability space for passwords (e.g. c1Bkanpurtis2&e% is just as probably as 1Bankruptcies2&%)
  • in reality, an attacker can use a dictionary, add in capitals, numbers, and digits, and get to this guess much faster than the calculated bits of entropy would imply
  • all the shown passwords are relatively easy to guess

Password managers

  • store passwords

  • sync passwords among your devices

  • generate random passwords

  • autofill passwords

  • protected by a master password

  • security and risks

    • single point of failure
    • master password capture, online guessing, or offline guessing
    • risk if passowrd manager fails

Lastpass

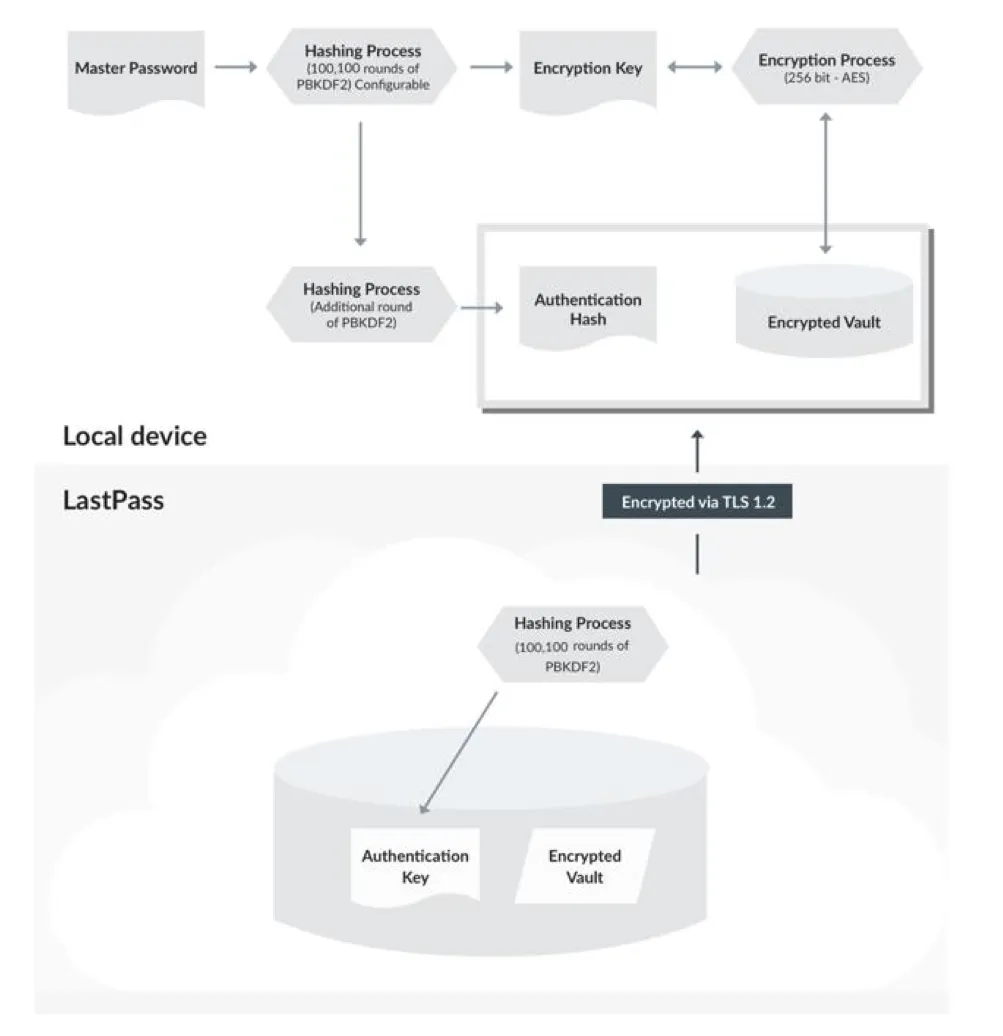
lastpass

  • puts your master password through a key derivation function, PBKDF2, for many rounds

  • this results in an encryption key that is used to encrypt the password vault, using AES

  • one more round of the KDF provides the authentication hash

  • key point: if an attacker steals your vault (which has happened with LastPass), and you used a weak master password, they can brute force that password to recover your vault

  • see LastPass Technical whitepaper for more details

1Password

  • k = PBKDF2(password, secret_key, 650000)

  • mixes a secret key with the password

  • to decrypt your vault, you need (a) password, (b) secret key, (c) encrypted vault

  • prevents a brute-force attack on your vault if it is stolen

  • this means you need to store the secret key safely and then enter it to authorize a new device to access your vault

  • 1Password recommends printing and storing it somewhere (they call this the Emergency Kit)

  • see 1Password Security Design for more details

Academic literature on password managers